By	Casey Muratori

Last time, in part one of this two-part post, I explained how repeated applications of common half-pel filters produce unusable images, and then I introduced a new filter that didn’t have this problem. It was a little bit blurrier than one might want. It was better than the alternatives  —  in fact it was the filter that shipped in the original version of Bink 2. Due to always having piles of other work to do, I never had a chance to revist the design and explore it further. But now that I am making the time to revisit this filter and write it up, I get to finally ask the question: is there a less blurry filter that still maintains the “infinitely stable” property? Spoiler alert: the answer is “probably not” and “definitely, here it is”. But before we get to why there are two answers to that question, and what they mean, let’s take a minute to make a better test bed.

When I originally worked on this problem, I had no idea what I was looking for. I didn’t even know that there was such a thing as an “infinintely stable” half-pel filter, so I wasn’t designing a system to find one. Instead, I was just making something that would run “many” iterations of a filter so I could look at it. All the images from part one reflect this methodology: the image slides from right to left a half-pixel at a time, so if you apply the filter 100 times, the final image will be displaced by 50 pixels. Now that we know what we’re actually looking for, we can be a little more precise. After two applications of a half-pel filter, we have moved the image exactly one pixel. Thus, if we just move the image one pixel backward, we can keep it in the same place. This makes a much nicer test, because not only can we apply the filter as many times as we want without worrying about the image “sliding off the screen”, but we can also difference the image against previous versions and against the original. This lets us test filters automatically. We simply apply the filter repeatedly and look for one of two things: convergence to an unchanging image that indicates the filter is infinitely stable, or sufficiently large deviation from the original image to indicate that the filter has “exploded”. For purposes of these tests, I chose “sufficiently large” as an average error per channel of 64 (out of 255), or a maximum error in any channel of a full 255. If either of those conditions were hit, the filter was considered to have “exploded”.

OK, now that we have a better idea of how to test these filters, let’s take a fresh look at the filters from part one. We’ll start with bilinear, which of course is not very interesting:

That’s after 244 iterations. As you might expect, it’s slow to “explode” because it’s always averaging pixels. But even it eventually hits the average error cap. Here’s h.264:

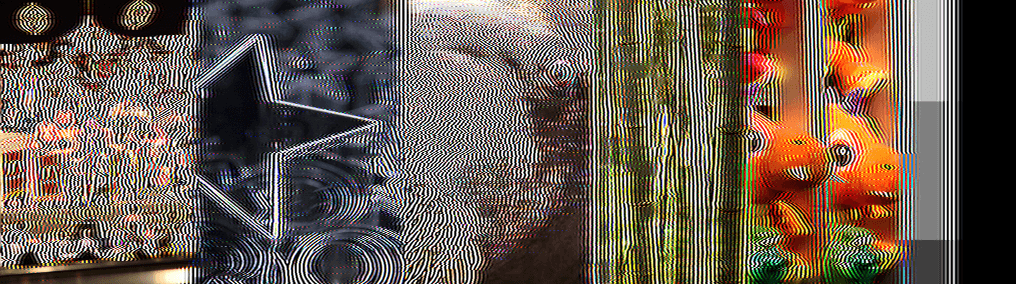
It takes only 78 iterations to explode. The 8-tap HEVC filter fairs slightly better, but still explodes after 150 iterations:

Lanczos at 6 taps explodes after 166:

And that’s all our exploding filters. That leaves just my integer filter left:

As expected, it’s the only one that doesn’t explode. It converges to an infinitely stable image after 208 iterations. So that’s pretty exciting right there  —  we now know, at least for a wide range of relevant test images, that this filter is actually infinitely stable, meaning that it will never produce an artifact no matter how many times you apply it. But that brings us back to our original question: is it the best we can do? And of course, you already know the answers, because I spoiler’d them at the beginning of the article: “probably not” and “definitely, here it is”. Let’s cover the “probably not” part first.

OK, so back in part one I mentioned that the filter kernel I came up with was the “best I could find” subject to a caveat. Here comes the caveat: When I was looking for that filter, I wasn’t actually looking for the best filter. I was looking for the best filter that could be expressed in terms of a very small number of integer shifts, adds, and subtracts. That may sound weird, but bear with me. You may have noticed that when I showed the coefficients for the h.264, HEVC, and bilinear filters, as well as my filter, I wrote them all as integer numerators over integer denominators, like this:

But I didn’t do that for windowed sinc  —  I wrote it like this:

The reason for this is that windowed sinc is actually derived from a continuous mathematical function that has nothing to do with basic integer ratios. When you apply it, you are using floating point to (as accurately as possible) represent the sinc function values. If you’re trying to apply it accurately, you don’t want to round it to simple fractions, because that will introduce error. Video codec filters traditionally couldn’t afford to do things this way. Floating point multiplies on something as intensive as motion compensation simply wasn’t feasible when you consider that video codecs were meant to be easily implemented in special-purpose hardware. This is especially true if you’re talking about industry-standard codecs that are supposed to run across a wide variety of devices including low-power, low-cost embedded chips. Furthermore, even when you’re on a CPU, the SIMD nature of modern instruction sets means that integer operations may still be faster on the CPU depending on what you’re doing: you can fit two 16-bit integers into the space of one 32-bit float, effectively doubling your operational throughput, so depending on the exact cycle counts of the operations you need in floating point vs. integer, floating point isn’t necessarily the fastest option. Now you can see why this caveat was important. Because I was targeting simple 16-bit integer operations only, I looked exclusively at kernels that could be expressed with small integers over power-of-two divisors up to 64, and no more. This is a much more constrained set of filters than if I had been looking at any set of 6 floating point coefficients. Similarly, for efficiency reasons, I didn’t consider any other number of taps. 6 or less was the only thing on the table, so I didn’t even test 8 or 10 tap versions. Thus we come to the first answer: “probably not”. If you continue to abide by these constraints, I don’t think there’s a better filter you can construct that can still be applied an infinite number of times and not degrade. The filter kernel in part one is probably the best you can do, although admittedly I haven’t tried to exhaustively prove it. But what if we don’t need to abide by those constraints?

If we get rid of the concerns specific to the original version of Bink 2 (now quite old  —  it has gone through many revisions since then), and use arbitrary floating point coefficients, how much better could we do? Well, since we know my integer-based kernel never degrades, and we know that Lanczos is sharper but does degrade, intuitively we should be able to find the place in-between the two sets of coefficients where degradation starts. So I made a program to help me look for exactly that point, and here’s the kernel I found:

This kernel takes 272 iterations to converge, but is infinitely stable and looks much sharper than my integer filter:

In fact, it’s almost indistinguishable from the original:

Almost… but not quite. If you look closely, you can still see some blurring and ghosting in high-contrast areas. Easy places to spot are the eye of the orange “dinosaur” and the bright light patches behind the bamboo. So the 6-tap float filter is definitely better, but it’s not perfect. Can we do better still?

The original choice of a 6-tap filter was made for the same reasons as the choice of small-integer fractions: I was looking for an extremely efficient filter. But since we’re exploring here, and have already moved to floats, why not look at a wider filter, too? Combining our 6-tap integer filter with a 6-tap Lanczos produced a really nice filter. What if we combined it with an 8-tap Lanczos instead? 8-tap Lanczos looks like this:

Like 6-tap Lanczos, it is also highly unstable and explodes after 178 iterations:

If we search in-between my 6-tap integer filter and the 8-tap Lanczos for a better filter, we arrive at this rather remarkable 8-tap filter:

As an infinitely-stable filter, it performs shockingly well. It converges after 202 iterations (a faster convergence than either of my other two filters), and looks so much like the original that it can be hard to guess which one is which:

Here’s that original again, for reference:

Compared to my original integer filter, this is clearly a dramatic improvement.

I was going to close this blog post with something like this:

That was the plan, anyway. But between writing part one and part two, I happened to e-mail the improved filter results to Fabian Giesen and Charles Bloom, and they (unsurprisingly) knew the math necessary to explore the issue analytically. It turns out there is literally eigenvector and eigenvalue analysis for filters, it’s just not quite done the same way. But you can do it easily  —  it’s actually built into CAM packages as a trivial one-step process  —  and you can actually look at the eigenvalues for the filters. This doesn’t give you the complete answer, because the fact that these filters round (or truncate) back to 8-bit (or 10-bit, or 12-bit) after every round is important, since the truncation changes the way errors accumulate as compared to infinintely precise algebra. Unfortunately, since this is definitely not my area of expertise, I don’t feel even remotely qualified to give an overview of any of this analysis. I asked both Fabian and Charles if they’d write up posts with all the good stuff they sent me in e-mail (they both have tech blogs  —  the ryg blog and cbloom rants), and to our great benefit Fabian ended up doing an awesome series on the math behind stable filters. If you’re interested to know the theoretical underpinnings of what’s been going on in these two blog posts of mine, I highly recommend checking it out!