| By | Casey Muratori |

and turn it into this:

after only a single second of video. It slid to the side like it should, since each frame moved the image a half pixel over. But instead of looking like a displaced version of the original image, the result appeared severely mangled.
Now, a “single second of video” is actually a lot of filter applications — 60 of them, actually, if it’s at 60 frames per second. But ideally we’d have filters that stand up to this kind of abuse. If we did, smoothly-scrolling videos wouldn’t have to be encoded with as many artifact corrections, so they’d be smaller, or higher quality, or both.
If you’re familiar with video compression, you might rightfully be wondering why you need to apply a half-pel filter more than once anyway. After all, if you do two half-pel filter applications, you’ve moved by one whole pixel, so why not just use the data from two frames ago and grab that?
Well, the answer is two-fold. First, the more data you need to encode for the fetch, the less compression you get. So if you start having to encode lots of “which frame to grab from” data unnecessarily, you won’t compress as well.
But that’s not that big a deal. The real issue is that if you need to grab from prior frames, you have to store them. Storing 2 prior frames instead of 1 uses, as you might guess, twice as much memory. This isn’t a big deal on a modern CPU that has tons of memory and just wouldn’t care. But it is a big deal if you’re trying to be a fast, portable, widely applicable video format that wants to run on devices where memory is tight (cell phones, embedded hardware, etc.)
For our purposes, we really didn’t want to have to store multiple frames for motion compensation just to work around the half-pel filter. So I was tasked to find out exactly what was going on here, and see if I could design a filter that wouldn’t have these problems.
I had never looked at filters before at all — literally. I had no idea how people typically designed them. Strangely enough, this turned out to be a good thing, because it meant I looked at the problem without a lot of preconceived notions.
The Basics
What you’ll learn very quickly if you look into half-pel filter design is that the common ones all take the same form: somewhere between 2 and 8 pixels of the input image are sampled and blended together at specific ratios to produce each pixel in the output image. They differ only by how many input pixels they use (often called “taps” in filter slang) and the ratios at which those pixels are blended. These ratios are often called the “filter kernel”, and it’s all you need to completely define the filter.
If you’re familiar with any kind of image sampling or resampling (like image scaling), then this should sound familiar to you. The filters are basically the same. Since video compression is a broad field with lots of research in it, there are obviously many other ways people do motion compensation that has nothing to do with simple filtering. But the codecs in common use tend to have motion compensation routines that include half-pel filters that are basically the same as image scaling filters: you just take your input pixels, multiply them by some weights, add them together, and you’ve got your output pixels.
The Need for “Sharpening”
OK, so you need to shift an image by a half a pixel. If you’re a graphics programmer, but you’re not particularly familiar with filtering, you might be thinking, “big deal, just bilinearly filter it”. That’s a standard thing we do in graphics when we need to produce in-between values from two inputs, like we’re doing here.
A bilinear filter for an exact half-pixel movement is easy to describe as a filter kernel — it’s just this:
It works, but it has some issues. If your primary goal is high-quality imaging — which is precisely the goal in video compression — the bilinear filter isn’t the best you can do, because it tends to introduce more blurriness into the result than is necessary. It’s not much, but it’s more than other filters you could have used.
To give you a visual idea of what I mean, here is a close-up of the walrus eye from the original image after a single application of some common filters:

On the far left is the original, and on the far right is bilinear. In the middle are some widely-used video codec half-pel filters. Hopefully, if you look closely, you can see that pretty much all the images look similar except for the bilinear, which looks a little bit blurrier. While it’s not a huge amount of blurring, it’s enough that if image quality is your primary goal (like it is in video encoding), you’d prefer one of the other filters.
So how are these other filters “keeping” the sharpness of the image and avoiding the blur? Well, recall that the bilinear blur kernel looks like this:
It’s very simple. To shift an image over by half a pixel, you take a pixel and blend it 50% with its neighbor. That’s it. Intuitively, you can imagine how it “blurs” the image, because in places where you might have had a bright white pixel next to a dark black pixel, those two pixels will get averaged together during the bilinear filter, and produce a gray pixel, “softening” the edge. This is happening at every pixel, so literally every place there was a pronounced difference in color or brightness, it is getting smoothed.
This is why higher-end video codecs don’t rely entirely on bilinear filtering for motion compensation (although it may still be used for some parts). Instead, they prefer filters that try to preserve the sharpness, like this:
As you can see, whereas bilinear filtering only looked at two pixels, these filters look at six (for h.264) or even eight (for HEVC) pixels. Furthermore, they don’t just compute basic weighted averages of those pixels — they use negative weights on some pixels to subtract those pixels away from the other values.
Why are they doing this?
It’s actually not that complicated to get a basic understanding: by using both positive and negative weights, and looking at a wider window, the filter is able to take the difference between neighboring pixels into account, and model the sharpness of the two cloest pixels relative to their further-away neighbors. This allows the result to preserve sharpness where pixels were changing dramatically from their neighbors, while still using averaging to produce plausible values for the “half pixel” shift that must necessarily reflect a combination of the pixels from the input.
Unstable Filtering
OK, so, problem solved, right? Well, perhaps if you’re only going to perform a single half-pixel shift and call it a day. But these “sharpening” filters (and I’m using that term very intentionally here) are actually doing something very dangerous that is essentially equivalent to what bilinear filtering is doing. They’re just do a better job of hiding it.
Where bilinear filtering reduces the sharpness in an image, these common filters enhance it. They are actually sharpening the image, just like the “sharpen” operation in your favorite photo editing package might do. The amount of sharpening is very slight, so if you only run the filter once, you won’t notice it. But if you run the filter more than once, it can become quite noticeable.
And unfortunately, because this sharpening is procedural and based on the differences between pixels, it creates a feedback loop that will continue to sharpen the same edge over and over and over until it destroys the image. To make this more concrete, take a look at some examples.
Here is the original image on top, with a bilinear filter run for 60 frames on the bottom:


As we would expect, the blurring just continues to reduce the sharpness of the image until it is quite smooth. Now here’s the original on top, and the h.264 half-pel filter run for 60 frames on bottom:


See all the garbage? It’s done the same thing as the bilinear “blurring out the image” effect, but in the opposite way — it has “sharpened out the image” so that every place there were details, there are now severely ringing light/dark patterns.
Does the HEVC codec do any better by using 8 pixels? Well, it does better than h.264, certainly:

but if we crank up the time from 60 frames (1 second) to 120 frames (2 seconds), we can still see that it is clearly feeding back and destroying the image:

For those of you who like signal processing sorts of things, before we move on to the next section, I’ll also throw in a windowed sinc function (called a Lanczos filter) for reference:
Why anyone would care what a “windowed sinc” looks like here is beyond the scope of the article, but suffice to say, it’s a popular filter for theoretical reasons so here’s what it looks like at 60 frames (1 second):

and at 120 frames (2 seconds):

Better than h.264, but about the same as HEVC.
Stable Filtering
How could we do better than h.264, HEVC, and windowed sinc? And how much better could we do?
These are questions I would have expected to see in the video compression literature, and be widely known by video compression experts, but actually — at least in 2011 — I don’t know of anyone who has even stated that this was a problem. So I was left to my own devices to devise a solution.
Fortunately, the problem statement is very straightforward: make a filter that you can apply as many times as possible while keeping the image looking roughly the same as it did when you started.
I thought of this definition as “stable filtering”, because to me, it could be considered a property of a filter. A filter is “stable” if it does not feed back on itself, so it can be applied over and over and not produce artifacts. A filter is “unstable” if it produces artifacts that magnify with successive applications, eventually destroying the image.
Again, why this isn’t already a thing in video codec or image processing literature, I don’t know. Maybe they have another term for it, but I haven’t seen it. The concept of “feedback” is well established in audio, but it just doesn’t seem to be a central concern in image processing, perhaps because filters are normally only meant to be applied once?
Were I an expert in the field, I would probably have an opinion about all of this, or perhaps even know of the nooks and crannies in the literature where solutions to this problem already exist but aren’t widely cited. But as I said at the outset of the article, I’d never done filter design before, so I was only looking at the common, widely-cited papers (although it’s worth noting, there was at least one person well-versed in the literature at RAD at the time and he hadn’t heard of anything like this either).
So there I was, having been told in the morning that we needed this filter, and I sat down that afternoon to try to design one. My approach was simple: I made a program that ran the filter hundreds of times, outputting the image each time, so I could look at the result of long runs. I then tried various filter coefficients and observed the results. It was literally just guided trial-and-error.
After about an hour, I had zeroed in on the best filter coefficients I could find for this task (with one caveat that I’ll discuss in part 2):
This kernel is on the edge between sharpening and blurring. Because sharpening will always feed back to bright, obvious artifacts, this filter kernel prefers slight blurring so that the image will just appear “duller”.
Here’s what it looks like after 60 frames. For reference, I’ve shown all the filters in this order: original (no filtering), mine, bilinear, Lanczos, h.264, HEVC:






As you can see, my filter does get a little blurrier than the sharpening filters, but it has no objectionable sharpening artifacts like they do after 60 frames. However, maybe you would prefer sharpening artifacts to blurring artifacts, so maybe it’s a toss up for the best sharpening filter (Lanczos) vs. mine. However, if we go to 120 frames, it becomes no contest:






After 300 frames, every filter other than mine is a joke:


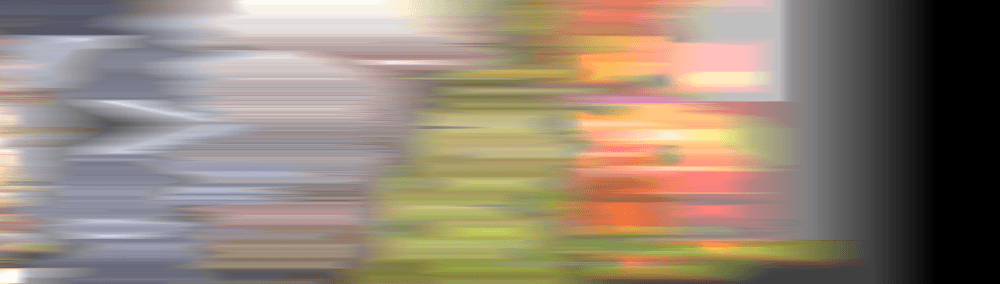
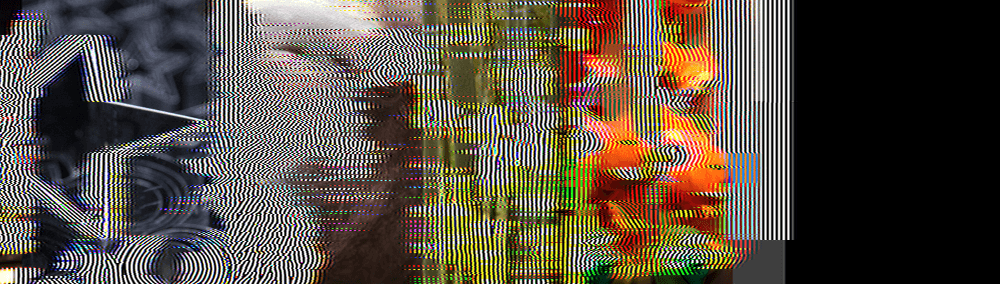

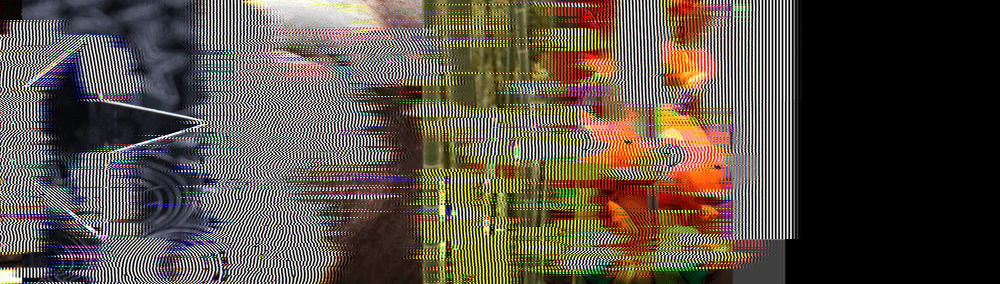
After 600 frames, the joke is even more cruel:


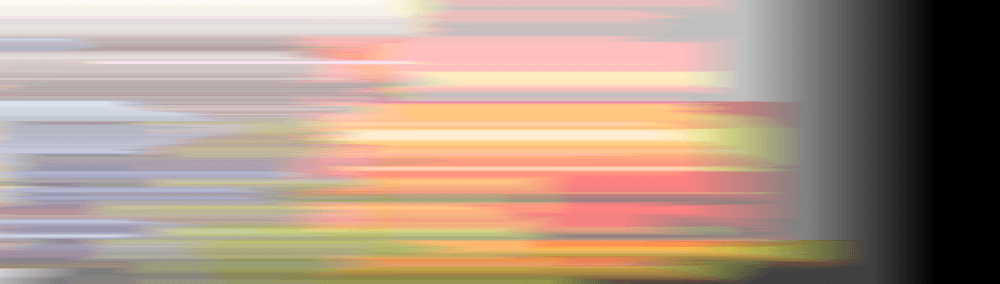
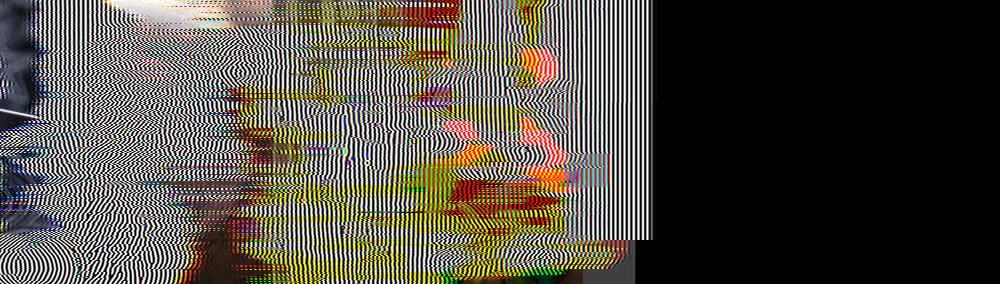


After 900 frames, well, why even bother:

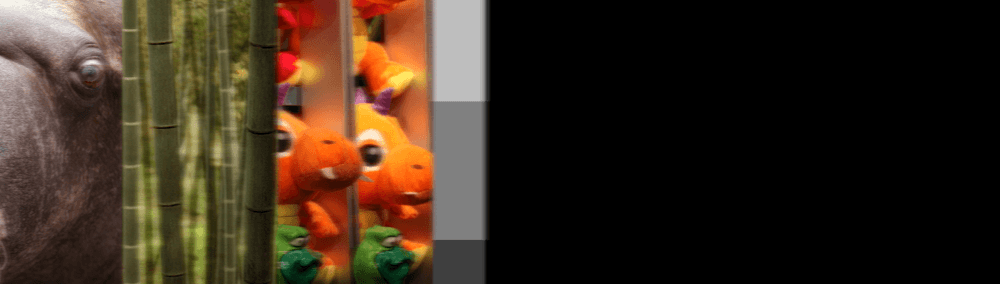
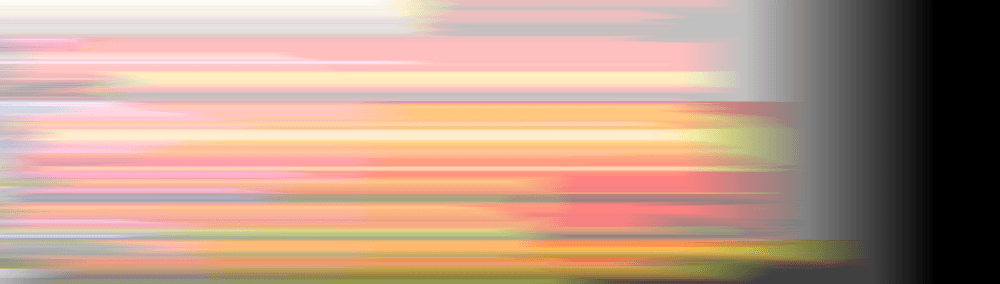
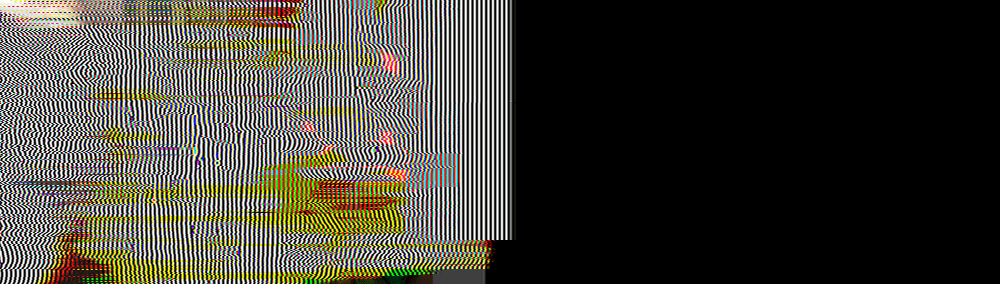

How Stable Is It?
At this point, the natural question would be, is my filter actually stable, or is it just a very slow blur, much slower than bilinear? If applied perhaps thousands of times, would my filter eventually blur out the image?
Surprisingly, the answer appears to be “no”. Although some blurring is introduced in the first hundred or so applications, it appears to converge to a stable image representation that never degrades thereafter. Here, for example, is another closeup of the walrus eye:

From left to right, that’s the original, then my filter applied 60 times, 120 times, 300 times, 600 times, and 900 times. As you can see, the blurring appears to converge to a stable state that no longer degrades, even with hundreds of additional applications of the filter. Contrast this with windowed sync at the same tap count, and you can see how badly (and quickly!) the artifacts feedback on themselves and create an unusable result:

My filter seems very stable, and also seems to produce the best looking results after successive applications, as compared to any existing filter I have seen. It seems to have some sort of “asymptotic” property, where it converges to a (boundedly) smoother image quickly and then preserves that smoother image, rather than having an apparently unbounded worst case that degrades to garbage.
I have even tried running the filter for a million applications, and it doesn’t seem to degrade any further than it does after the first few hundred. Without better mathematical analysis (and I’ve yet to find the math that would work to prove this definitively, although I’m sure it’s out there somewhere), I can’t say for certain that somewhere in the billions or trillions of applications it doesn’t somehow break. But within the limits of reasonable testing, I can’t find any further degradation.
Is This the Best Stable Half-pel Filter for Six Taps?
So the obvious thing to do at this point is to ask, “Is this the best we can do?” Intuition would suggest that the answer is “no”, because with literally no background in filter design and a near-complete ignorance of the literature, I came up with this filter after an hour. One would at least assume that such a short exploration shouldn’t have found the final-ultimate-best-answer-of-all-champions-majesty filter.
Is that assumption correct? And if it is, what is the final ultimate best answer of all champions? I’ll cover this in detail in Stable Filtering - Part 2, so stay tuned.