By	Casey Muratori

A decade and a half ago, in 2001, I was trying to increase the flexibility and performance of the animation compositor in Granny 3D. The biggest sticking point was the use of quaternions as the underlying rotation representation, because as everyone “knew” at the time, you could not treat them simply as 4D vectors that could be polynomially combined. Polynomial combinations are crucially important for animation compositing, because they allow you to “mix” animation from many sources at once while providing order independence (so the result of a composite will not depend on what order you happen to apply the individual parts). You can easily do this with positions, since they are just 3-vectors that can be multiplied by coefficients and added together at will. On the other hand, orientation quaternions, since they were constrained to live on the surface of a sphere, could not. Or could they? In order to find an answer, I made a visualization program that allowed me to compare the axis sweeps of multiple rotation methods at the same time: quaternion linear interpolation (red), quaternion spherical linear interpolation (green), and the exponential map (blue). I made them additive, so that if two curves overlapped, their colors would combine. As one might expect, for small rotations, all three methods produced nearly identical results, and the curves were white:

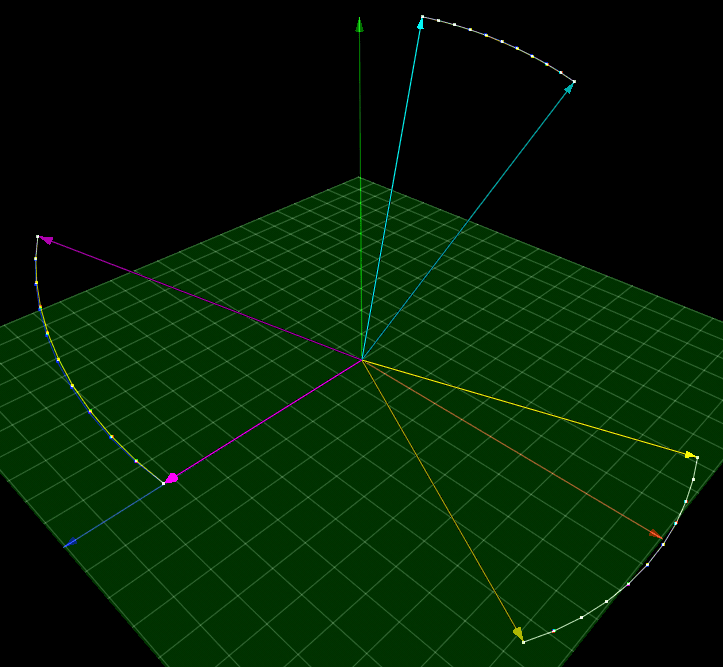
However, to my surprise, larger rotations produced very little divergence between linear and spherical interpolation, despite substantial divergence for exponential map interpolation:

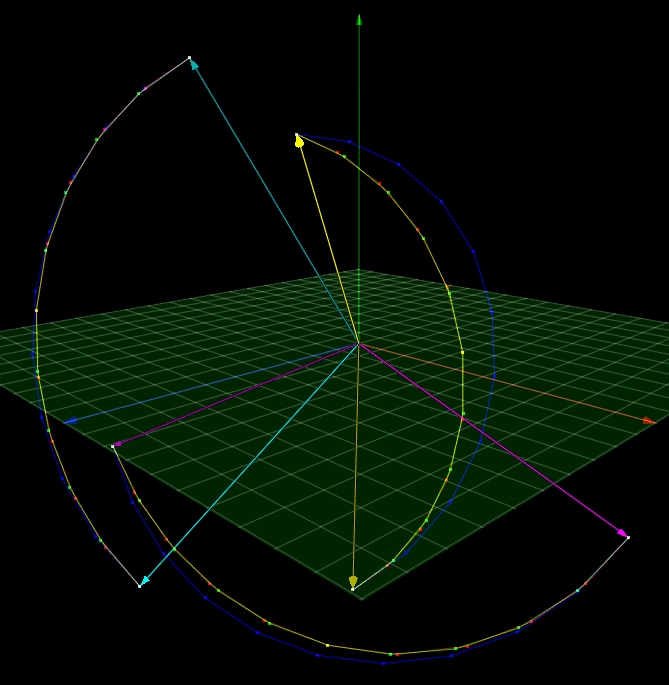
The more I played with it, the more I realized that I had been thinking about the problem all wrong: not only are linear and spherical interpolations or quaternions always exactly the same path, but because of the half-angle construction of quaternions, their speeds are much more similar than you would expect from linear interpolation of whole-angle rotation representations like matrices. Even extreme differences in interpolation between spherical interpolation and the exponential map yielded substantively little difference between spherical interpolation and linear interpolation of quaternions:

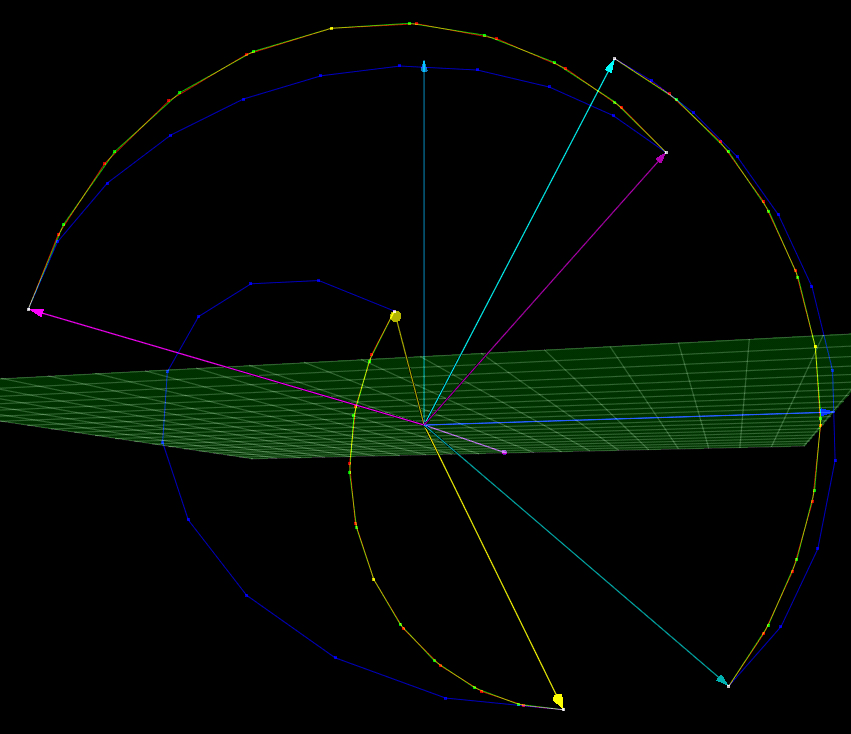
This visualization-driven realization informed the entire design of the 2.0 version Granny 3D animation engine. Aided by a much better and more intuitive understanding of how quaternions really worked, I was able to develop a number of novel techniques that allowed the animation core to be much faster and more flexible. Several years later, in 2006, I put up a makeshift video describing one of the more obscure tricks I employed. Because quaternions differentiate between 360 and 720 degree rotations (unlike matrices), with a little preconditioning you can make joints behave much more realistically under animation compositing as they would with any other orientation representation:

If you have a quaternion-based animation engine, I highly recommend using this method! It costs nothing and yields much more predictable and satisfying animation blending results for rotational joints in all cases.